C#で解くLeetCode「198. House Robber」

概要

エンジニア職での就職・転職では会社によってはコーディングテストというものがあります。
新卒でも中途でも入社したい会社というのは誰でもいい環境を求めるのではないでしょうか。
そこで、コーディングテストで振り落とされないためにもLeetCodeというテスト対策ができるサイトでアルゴリズム力を鍛えたいと思います。

問題

198. House Robber

あなたはプロの強盗で、ある通り沿いの家々を襲う計画を立てています。各家には一定額のお金が隠されています。あなたが各家を襲うのを阻む唯一の制約は、隣接する家にはセキュリティシステムが接続されており、同じ夜に隣接する2つの家が侵入された場合、自動的に警察に連絡されることです。

各家の金額を表す整数配列 nums が与えられたとき， 今夜，警察に通報することなく強盗できる最大金額を返せ．

制約

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 400

解説

再帰的な関係の把握

例題から[2,7,9,3,1]の問題を使用して解説していきます。
初めにどのようなパターンがあるかを把握しましょう。
最初の分岐点は1番目の家に「入る」「入らない」の二つです。
まずは１番目の家に「入る」パターンをツリーを作成しながら確認していきましょう。

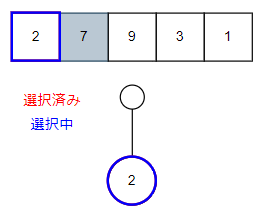
このようなツリーとなりました。
次は2番目の家ですが、1番目の家に入ってしまったのでスキップします。
次に確認する家は3番目と4番目の家です。
3番目の家に入ったら4番目の家には入れません。逆に4番目の家に入るためには3番目の家はスキップする必要がありますので、どちらかを選択する必要があります。
今回はツリーの作成を目的としているのでひたすらツリーを伸ばしていきましょう。

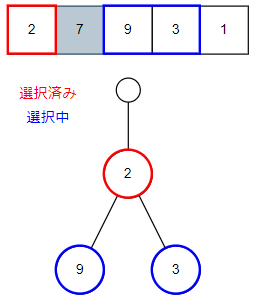
このようなツリーとなりました。
次は3番目の家に入った場合ですね。

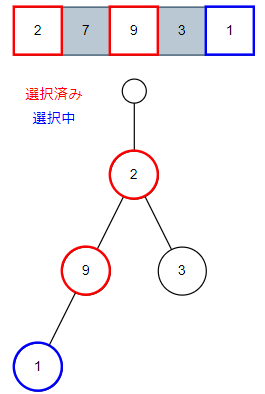
このようなツリーとなります。これ以上伸ばせないので1番目と４番目に入った場合のツリーを確認しましょう。

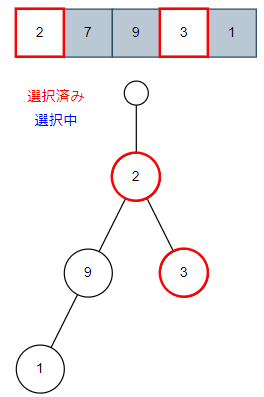
こちらもこれ以上伸ばせそうにありませんね。
では最初に戻って1番目の家に入らずに2番目に入った場合どのようなツリーとなるか同じように確認していきます。

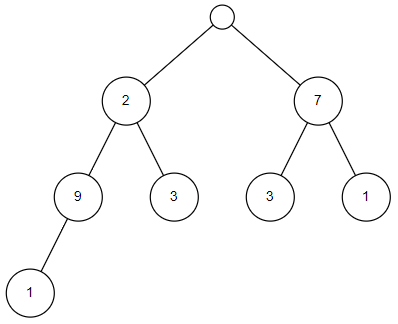
最終的にこのような図になりました。おなじみの二分木です。
今回はどのパターンで家に入ると一番大きな値になるかという問題なので、2択の内どちらかの合計値が大きいかという判断をすると最終的にどのパターンが大きい値となるかが求められます。
つまり、DFS探索を帰りがけ順 (post-order) で合計値を比較すると求められることが分かりますね。
図で確認してみましょう。

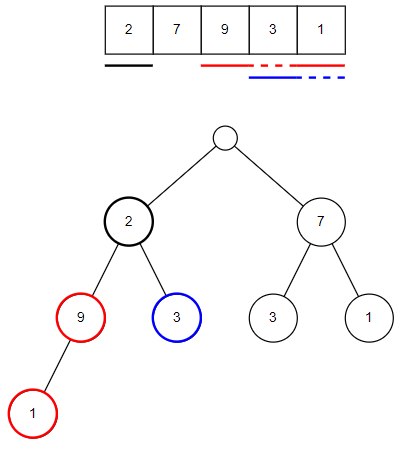
まず初めに小さな二分木から確認していきましょう。このパターンだと1番目の家に入った後を比較します。
『赤の合計値』と『青の合計値』どちらが多いでしょうか。10と3なので赤が多いですね。
次は２番目の家に入った後を比較します。

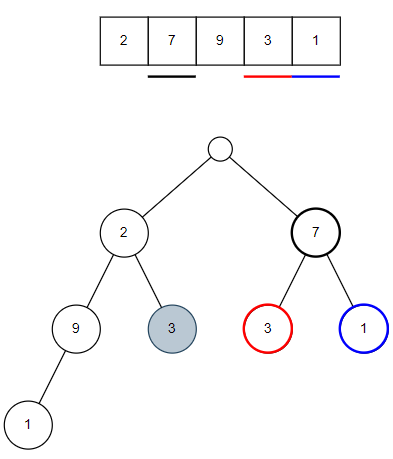
『赤の合計値』と『青の合計値』どちらが多いでしょうか。3と1なのでこれも赤が多いですね。
次は最初の選択肢まで戻り比較していきましょう。

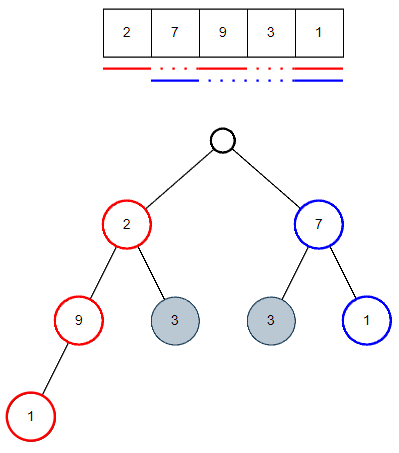
『赤の合計値』と『青の合計値』どちらが多いでしょうか。12と8なのでこれも赤が多いですね。
これでどの家を選ぶと最大値となるのかが求まりました。
流れを理解したら次はコードに表すための式を求めます。

式の求め方

最初の選択を例に出して式を書いていきます。

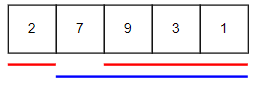
一番最初の選択は1番目の家に『入る』か『入らない』かでした。
入った場合と入らなかった場合を比較して大きい方が合計値が高いものとなります。
sum = max("入る場合", "入らない場合")

そして入る場合はnums[0]とnums[2]以降の最大値となります。この『nums[2]以降の最大値』というのが再帰的な処理になります。つまりこのような式となります。
sum = Max(nums[0] + Rob(2:n), "入らない場合")

入らない場合は2番目以降の最大値なので最終的にこのような式となります。
sum = Max(nums[0] + Rob(2:n), Rob(1:n))
iを使用するとこうですね。
sum = Max(nums[i] + Rob(i+2:n), Rob(i+1:n))

再帰的な処理のままだとDFS探索となってしまいますが、ここで終わらせずにDP(動的計画法)を使用して改善ができないか検討しましょう。

DPを使用した改善

今回再帰的な処理となっているのはRob(i:n)の部分列の処理です。
この部分列をDPを使用して解決していきます。
まずは1番目までの値の最大合計値を求めましょう。

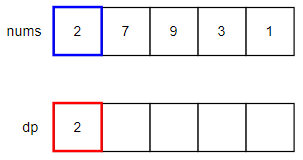
値は2の1つしかないので自然と最大値は2となります。最大値が求まりましたらdpを表す配列に格納しましょう。
次は2番目までの値の最大合計値を求めましょう。

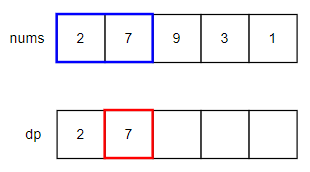
2番目までの数字は2と7がありますが、隣り合う値は合計できない制約があるため、7が最大値となります。
次は3番目までの値の最大合計値を求めましょう。

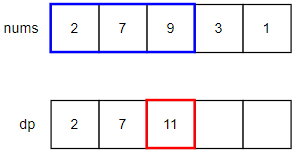
3番目までの数字は2, 7, 9がありますが、引き続き制約があるため2, 7, 9, 2+9のいずれかになります。最大値は2+9の11となります。
この際、2を使用するのはdp[i-2]ということを注意してください、次の図で説明しますので飛ばして最後までの値の最大合計値を求めましょう。

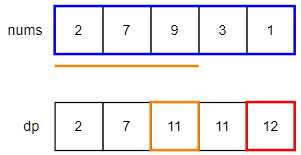
最後までの数字のパターンはいくつもありますが、先ほどの式を思い出してください。
sum = Max(nums[i] + Rob(i+2:n), Rob(i+1:n))
しっかり理解できた方なら気付いたとおもいますが、この式がdp[i]の選択肢1に相当します。
つまり『現在の位置』と『2つ先以降の値の最大合計値』です。順番が前後していますが同じ形になっていますので当てはめてみましょう。

まず『現在の位置』、これはnums[i]となります。
次に『2つ先以降の値の最大合計値』、今回は前から探索しているので、『2つ前以前の値の最大合計値』に置き換えましょう。dpは『現在探索しているまでの最大合計値』が入っています。
ですので、オレンジ色のdp[i-2]が『2つ前以前の値の最大合計値』となるわけです。

つまりnums[i] + Rob(i+2:n)はnums[i] + dp[i-2]に置き換えることができます。順番が前後したことによってRob(i+2:n)がdp[i-2]に置き換わったようにRob(i+1:n)がdp[i-1]に置き換わります。

最終的にはこのような式になりました。
dp[i] = Max(nums[i] + dp[i-2], dp[i-1])
それではこの式をもとにコードに起こしていきましょう。

DP解法のコード化

まずはおなじみエラー処理のアーリーリターンです。
nums[]が空であれば何も盗めないので0を返します。

if (nums.Length == 0)
{
    return 0;
}

次に変数の用意です。dp[i]を求める際はnums[i], dp[i-2], dp[i-1]の3つの値を使用していました。num[i]は探索対象として取れるので、一時保存する必要のあるdp[i-2], dp[i-1]を『2つ前の値』、『1つ前の値』として変数を用意します。

int prev1 = 0;
int prev2 = 0;

探索の準備ができましたら探索処理を実装していきます。
今回の探索はnumsから値を一つずつ取り出しているので、foreachで値を取り出していきます。

まずは『2つ前の値』として『1つ前の値』を回避しておきます。
その後dp[i] = Max(nums[i] + dp[i-2], dp[i-1])を表す処理で現在までの最大値を求め、『2つ前の値』を更新します。

最後にdpの最後となる値を返して終了です。

foreach (var num in nums)
{
    int tmp = prev1;
    prev1 = Math.Max(prev2 + num, prev1);
    prev2 = tmp;
}

return prev1;

ソースコード

public class Solution
{
    public int Rob(int[] nums)
    {
        if (nums.Length == 0)
        {
            return 0;
        }

        int prev1 = 0;
        int prev2 = 0;

        foreach (var num in nums)
        {
            int tmp = prev1;
            prev1 = Math.Max(prev2 + num, prev1);
            prev2 = tmp;
        }

        return prev1;
    }
}