概要
エンジニア職での就職・転職では会社によってはコーディングテストというものがあります。
新卒でも中途でも入社したい会社というのは誰でもいい環境を求めるのではないでしょうか。
そこで、コーディングテストで振り落とされないためにもLeetCodeというテスト対策ができるサイトでアルゴリズム力を鍛えたいと思います。
問題
あなたはプロの強盗で、通り沿いの家々を襲う計画を立てています。各家にはある金額のお金が隠されています。
この場所の家はすべて円形に配置されているので、最初の家は最後の家の隣人です。
そして、隣接する家にはセキュリティシステムが接続されており、同じ夜に隣接する2つの家に泥棒が入った場合、自動的に警察に連絡されるようになっています。
各家の金額を表す整数配列numsが与えられたとき、警察に通報せれずに今夜強奪できる最大金額を返せ。
制約
1 <= nums.length <= 1000 <= nums[i] <= 1000
解説
こちらは198. House Robberを派生させた問題となりますので、解いていなければ198番の問題を先に解きましょう。
こちらの問題の解答を使用しますので、解法が分からなければ以下のリンクを確認してください。
 C#で解くLeetCode「198. House Robber」
C#で解くLeetCode「198. House Robber」
前回の問題との差
まずは問題のおさらいをしましょう。
基本的には同じですが、今回は円形に家が並んでいます。円形に並んでいることで、最初の家と最後の家には同時に入れません。
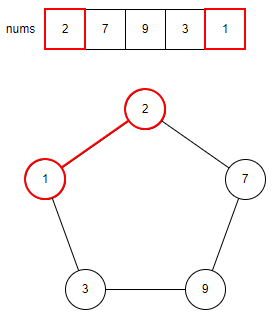
この制限を前回解いた問題に当てはめてみましょう。
前回比較していたのは『現在の位置の値と2つ先以降の値の最大合計値』と『1つ先以降の値の最大合計値』を比較していました。
以下の図が前回イメージした図です。
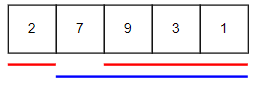
今回はさらに最初と最後の値を合計できないという制限が増えたので、以下のような図となります。
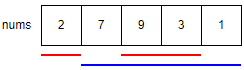
赤い線が変わり、青い線はそのままという結果になりました。
赤い線の部分の比較対象は『現在の位置の値と2つ先から最後のひとつ前の値の最大合計値』ということですね。
前回『2つ先以降の値の最大合計値』は『部分列』という説明をしました。
この『部分列』にどんな変更があるかというと、範囲が変わっています。
範囲を指定できるようにし、赤と青を比較して大きい方を返せば最大数が求まることが分かりました。
それではコードを修正していきましょう。
コードの修正
public int Rob(int[] nums)
{
if (nums.Length == 0)
{
return 0;
}
int prev1 = 0;
int prev2 = 0;
foreach (var num in nums)
{
int tmp = prev1;
prev1 = Math.Max(prev2 + num, prev1);
prev2 = tmp;
}
return prev1;
}こちらが前回使用した関数で、渡された配列の値から制約を守りながら最大合計値を求める関数です。
配列を渡すのと同時に範囲を指定できるように変更しましょう。
この関数は使用される側なのでLengthの確認処理は後程の関数に移動させます。
public int Rob(int[] nums, int lowIndex, int highIndex)
{
int prev1 = 0;
int prev2 = 0;
for (int i = lowIndex; i <= highIndex; i++)
{
int tmp = prev1;
prev1 = Math.Max(prev2 + nums[i], prev1);
prev2 = tmp;
}
return prev1;
}foreach文からfor文に変更して範囲を指定するだけですね。
次にこちらを利用して初めの二択を行いましょう。
public int Rob(int[] nums)
{
...
return Math.Max(Rob(nums, 0, nums.Length - 2), Rob(nums, 1, nums.Length - 1));
}先ほどの関数は制約を守っているので、制約を気にせずに範囲を指定することが可能です。
1番目から最後のひとつ前と、2番目から最後のインデックスを渡して大きい方を返す。
これだけでは0個と1個の場合に範囲外として例外が発生してしまうため、先ほど消した0個の場合の処理に1個の場合の処理を足して終了です。
public int Rob(int[] nums)
{
if (nums.Length == 0)
{
return 0;
}
else if (nums.Length == 1)
{
return nums[0];
}
return Math.Max(Rob(nums, 0, nums.Length - 2), Rob(nums, 1, nums.Length - 1));
}ソースコード
public class Solution {
public int Rob(int[] nums)
{
if (nums.Length == 0)
{
return 0;
}
else if (nums.Length == 1)
{
return nums[0];
}
return Math.Max(Rob(nums, 0, nums.Length - 2), Rob(nums, 1, nums.Length - 1));
}
public int Rob(int[] nums, int lowIndex, int highIndex)
{
int prev1 = 0;
int prev2 = 0;
for (int i = lowIndex; i <= highIndex; i++)
{
int tmp = prev1;
prev1 = Math.Max(prev2 + nums[i], prev1);
prev2 = tmp;
}
return prev1;
}
}